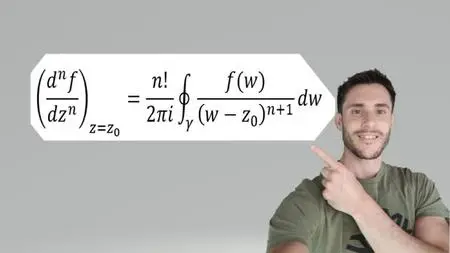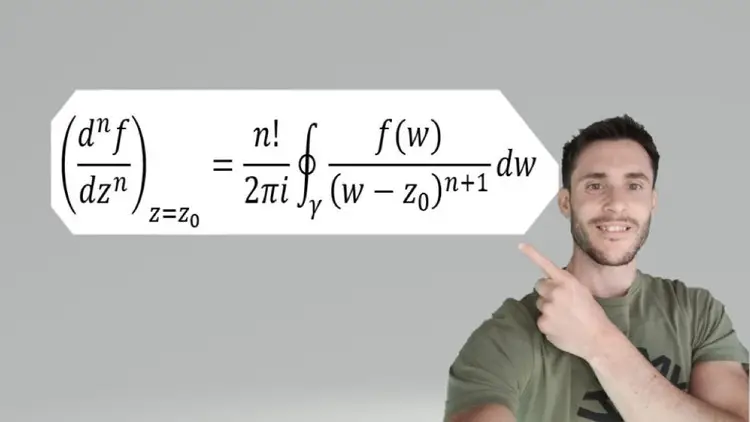Mastering Complex Calculus: From Derivatives to Residues

Complex Calculus: derivatives of complex variables, contour integration, Laurent series, Fourier series, and residues

What you'll learn
How to derive the most important theorems and concepts related to Complex Calculus
Cauchy's integral theorem
Cauchy's integral formula
Laurent Series
How to derive the Fourier Series from the Laurent Series
How to derive the Taylor Series from the Laurent Series
Residues
Contour integration
Requirements
Single Variable Calculus (especially: derivatives, integrals)
Multivariable Calculus (especially: Stokes' theorem, line integrals)
Description
Complex Calculus is an essential course that provides students with a foundation in complex functions,
derivatives of complex variables
,
contour integration
,
Laurent series
,
Fourier series
, and
residues
. In this course, you will learn the key concepts of Complex Calculus, and the process of reasoning by using mathematics, rather than rote memorization of formulas and exercises. Here's what you need to know about this course:
Introduction to Complex Functions
: The course begins by focusing on the concept of complex functions.
Derivatives of Complex Variables
: Next, the concept of derivative is extended to functions of a complex variable.
Contour Integration
: You will learn about contour integration, and the following theorems will be derived: Cauchy's integral theorem and Cauchy's integral formula.
Laurent Series
: The Laurent series will be mathematically derived. From Laurent, the Fourier and Taylor series are also derived.
Residues
: You will be introduced to residues and how to use them to do contour integration.
Prerequisites: To take this course, you should have completed single variable Calculus, especially derivatives and integrals, and multivariable Calculus, especially line integrals and Stokes' theorem.
Original Material
: This course is based on the instructor's notes on Complex Calculus, and the presentation of the results is therefore original.
Focusing on Understanding: The explanations are given by focusing on understanding and mathematically deriving the key concepts, rather than learning formulas and exercises by rote.
Benefits
: Some of the results presented in this course constitute the foundations of many branches of science, including Quantum Mechanics, Quantum Field Theory, and Engineering (in the Control theory of dynamical systems, for instance).
By mastering the contents of this course, you will be able to tackle the most interesting mathematical and engineering problems.
Who this course is for
: This course is suitable for anyone interested in expanding their knowledge of mathematics, including students of mathematics, physics, engineering, and related fields, as well as professionals who wish to develop their understanding of Complex Calculus.
Who this course is for:
mathematicians
physicists
engineers
computer scientists
Students interested in the concepts of Complex Calculus
Students who want to rigorously derive the concept of Fourier Series
Students who want to understand how to do contour integration


More Info