Geometric Algebra: The Math You Weren't Taught

Unifying Linear Algebra. Master Geometric Algebra for a true understanding of vectors, rotors & complex numbers

What you'll learn

• Master the core concepts of linear algebra: including vectors, linear transformations, matrices, and eigenvalues from an abstract and visual perspective.
• Understand the foundations of Geometric Algebra and how it unifies and extends linear algebra, complex numbers, and vector calculus.
• Develop powerful geometric intuition to interpret rotations, projections, and reflections using multivectors and the geometric product
• Build confidence with geometric thinking that goes far beyond what’s taught in standard math courses, empowering you to learn more advanced topics with ease.
• Apply Geometric Algebra to real-world problems in physics, engineering, and computer science — with hands-on examples and step-by-step derivations
• Translate between traditional linear algebra and GA formalisms, gaining a deeper understanding of both frameworks

Requirements

• A basic understanding of high school algebra (e.g. how to manipulate equations and work with coordinates).
• No prior knowledge of linear algebra or Geometric Algebra is required — we start from the ground up and build concepts progressively.
• Curiosity and a willingness to think visually and conceptually — this course emphasizes intuition as much as computation.

Description

Have you ever felt that mathematics is just a collection of disconnected rules and clever tricks?

You memorize the dot product for projections and the cross product for… something perpendicular (but only in 3D). You’re told to accept that the square root of -1 is ‘i’, a number that is purely “imaginary.” You grapple with matrices for transformations, quaternions for rotations, and tensors for anything more complex, each with its own separate set of rules.

It feels fragmented. It feels abstract. And deep down, you suspect there has to be a simpler, more elegant, and more unified truth holding it all together.

You are right. And that unification is Geometric Algebra.

Welcome to a course that will fundamentally transform your relationship with mathematics. My name is [Your Name], and as a PhD researcher specializing in Geometric Algebra, I’ve dedicated my career to understanding and teaching this revolutionary framework. I designed this course to take you from the familiar ground of linear algebra and guide you, step-by-step, into a world where mathematics becomes intuitive, visual, and profoundly interconnected.

This isn’t just another math course; it’s a paradigm shift.

In this course, you won't just learn new formulas. You will unlock a new way of thinking. You will discover:

• The one mathematical operation that makes the dot product, the cross product, and even the algebra of complex numbers emerge naturally from a single source. Forget memorizing three sets of rules; master one concept that contains them all.
• The true identity of ‘i’. We will strip away the "imaginary" label and reveal what complex numbers truly are: tangible, geometric objects that you can see and visualize, representing rotations in a plane.
• The secret to flawless rotations—in any dimension. You’ll learn to use "Rotors," the native language of rotation in Geometric Algebra, allowing you to sidestep the infamous gimbal lock that plagues engineers and 3D artists.
• How to literally 'divide' by a vector. An operation that is undefined in traditional algebra becomes a powerful tool in GA, allowing you to solve geometric equations with stunning simplicity.
• Why a single, elegant GA equation can replace the four famous Maxwell's equations of electromagnetism. This isn't just a party trick; it's a glimpse into the profound physical insights that a unified mathematical language can provide.

From Abstract Rules to Concrete Intuition

The single greatest advantage of Geometric Algebra is that it transforms the abstract, often confusing rules of traditional math into concrete, visual intuition. This course is designed to bridge that gap, turning your "black box" calculations into "aha!" moments of genuine understanding.

This is where the magic happens:

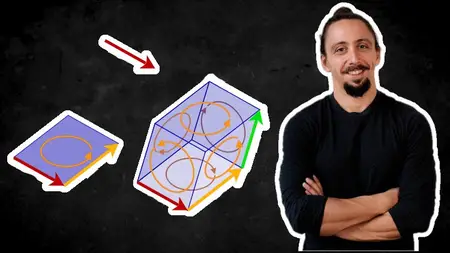
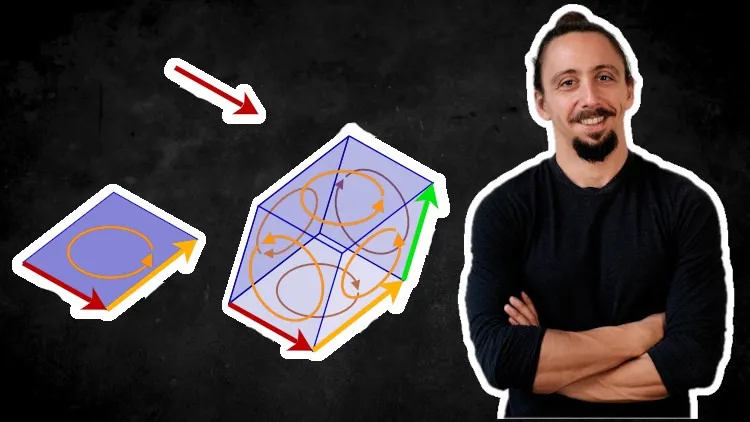
• You will no longer describe a 3D plane using an indirect, perpendicular normal vector. That method is counter-intuitive; you're defining something by what it's not. Instead, you will learn to represent the plane itself as a single, fundamental object—a bivector—that directly captures the plane's orientation and area.
• You will no longer perform rotations with an unintelligible matrix of sines and cosines. Forget plugging numbers into a formula and hoping it works. Here, you will command the very engine of rotation itself—a rotor—and understand visually how it sweeps objects to their new positions.
• You will no longer use a separate, 3D-only cross product to calculate things like torque or angular momentum. You will replace it with a universal "outer product" that gives you the true plane of rotation, a concept that makes physical sense and works in any dimension.
• You will no longer have to blindly accept imaginary numbers. We will strip away the mystery and show you what 'i' truly represents geometrically, transforming an abstract idea into a tangible tool you can visualize and use with confidence.

This is the power of a language built on geometry from the ground up. It’s the difference between following a cryptic recipe and finally understanding the art of cooking.

A Unified Framework for Modern Science and Technology

Geometric Algebra is not a purely academic curiosity. It is the engine behind cutting-edge applications in the most demanding fields:

• Physics: It is the natural language for Classical Mechanics, Electromagnetism, Relativity, and even Quantum Mechanics, providing a deeper, more intuitive understanding of spin.
• Computer Graphics & Robotics: It revolutionizes the handling of 3D objects and transformations, simplifying rendering algorithms, collision detection, and robotic kinematics.
• Engineering & Computer Science: It offers robust and efficient solutions for signal processing, machine learning on high-dimensional data, and complex system modeling.

By mastering the concepts in this course, you are not just learning math; you are future-proofing your skills and equipping yourself with the powerful toolkit that the next generation of scientists, engineers, and developers will use.

Your Journey to Mathematical Mastery

We will build your knowledge from the ground up. No prior experience with Geometric Algebra is necessary.

1. We begin by revisiting Linear Algebra through a powerfully intuitive geometric lens, ensuring you have a rock-solid foundation.
2. Next, we introduce the star of the show: The Geometric Product. You'll see how it elegantly unifies the dot and outer products.
3. We will then build a zoo of new geometric objects—bivectors, trivectors, and multivectors—and learn how to manipulate them.
4. From there, you will master rotations and transformations using rotors, seeing for yourself why they are superior to any other method.
5. Finally, we will put it all into practice with worked-through examples and real-world applications, solidifying your understanding and showing you what your new skills can do.

If you are ready to stop memorizing disconnected mathematical facts and start building a deep, intuitive, and unified understanding of the language that describes our universe, then this is the course you have been waiting for.

Who this course is for:

• Students and professionals in physics, mathematics, engineering, or computer science who want to go beyond standard linear algebra and explore a powerful, unified mathematical language.
• Anyone struggling to build geometric intuition from traditional matrix-based approaches and looking for a visual, conceptual understanding of vectors, transformations, and rotations.
• Curious learners interested in how Geometric Algebra simplifies and connects topics like complex numbers, quaternions, and vector calculus under one framework.
• Educators and autodidacts seeking a deeper and more modern approach to linear algebra that emphasizes clarity, elegance, and geometric meaning.
• Aspiring researchers and advanced students looking for the tools to work more effectively in fields like theoretical physics, robotics, computer graphics, and quantum computing.