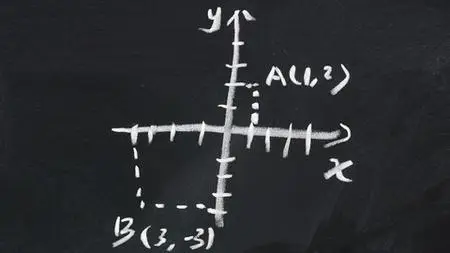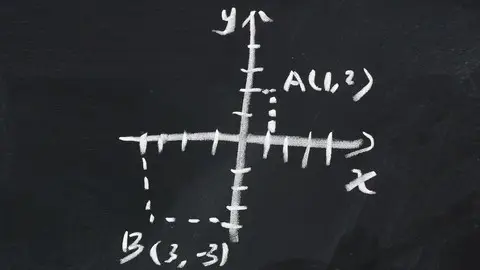Master The Fundamentals Of Complex Numbers
Last updated 12/2021
MP4 | Video: h264, 1280x720 | Audio: AAC, 44.1 KHz
Language: English | Size: 2.75 GB | Duration: 3h 4m
Last updated 12/2021
MP4 | Video: h264, 1280x720 | Audio: AAC, 44.1 KHz
Language: English | Size: 2.75 GB | Duration: 3h 4m
Master the Fundamentals of Complex Numbers
What you'll learn
Basic Complex Number Operations
Complex Roots of Polynomial Equations
Argand Diagrams
Modulus-Argument Form (Polar Form) of Complex Numbers
Euler's Formula
Loci of Complex Numbers (for IGCSE/College-Level)
De Moivre's Theorem (for IB/College-Level)
Nth Roots of a Complex Number (for IB/College-Level)
Problem-Solving involving Complex Numbers
Requirements
Be proficient to perform basic operations in indices, algebra, vectors (elementary level) and trigonometry
Description
Dear students,Welcome to this course "Master the Fundamentals of Complex Numbers"!This course is designed specially for students who are: doing college-level mathematics, taking their IGCSE/GCE A level or the IB HL Math examinations.At the end of the course, and depending on which exams you are taking, you will learn most/all of the following:basic complex number operationscomplex roots of polynomial equationsArgand diagramsthe modulus-argument form (polar form)multiplication and "division" of complex numberspowers of complex numbersEuler's formulaloci of complex numbers (for IGCSE/College-Level)inequalities of complex numbers (for IGCSE/College-Level)De Moivre's Theorem (for IB/College-Level)nth roots of complex numbers (for IB/College-Level)Along the way, there will be quizzes and practice questions for you to get familiarized with complex numbers. There are also several bonus lectures which will further enhance your understanding of the topic. If you encounter any problems, please do not hesitate to contact me for more clarifications. I hope that you will find this course useful in your academic pursuit. Enjoy the course! Cheers!Dr Ling M K Daniel, PhDoo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo oo
Overview
Section 1: Introduction to Complex Numbers
Lecture 1 Introduction to Complex Numbers
Lecture 2 Practice 1
Lecture 3 Practice 1 Answers
Section 2: Basic Complex Number Operations
Lecture 4 Basic Complex Number Operations
Lecture 5 Practice 2
Lecture 6 Practice 2 Answers
Section 3: Quiz 1
Section 4: Complex Roots of Polynomial Equations
Lecture 7 Complex Roots of Polynomial Equations
Lecture 8 Practice 3
Lecture 9 Practice 3 Answers
Section 5: Argand Diagrams
Lecture 10 Argand Diagrams
Lecture 11 Practice 4
Lecture 12 Practice 4 Answers
Section 6: Introduction to the Modulus-Argument Form of Complex Numbers
Lecture 13 The Modulus-Argument Form
Lecture 14 Practice 5
Lecture 15 Practice 5 Answers
Section 7: Multiplication and Division in Modulus Argument Form
Lecture 16 Multiplication and Division in Modulus Argument Form
Lecture 17 Practice 6
Lecture 18 Practice 6 Answers
Section 8: Powers of Complex Numbers
Lecture 19 Powers of Complex Numbers
Lecture 20 Practice 7
Lecture 21 Practice 7 Answers
Section 9: Introduction to the Euler's Formula
Lecture 22 Euler's Formula
Lecture 23 Practice 8
Lecture 24 Practice 8 Answers
Section 10: Quiz 2
Section 11: Loci of Complex Numbers (for IGCSE/College-Level)
Lecture 25 Loci of Complex Numbers and Locus of a Circle
Lecture 26 Practice 9
Lecture 27 Practice 9 Answers
Lecture 28 Locus of a Perpendicular Bisector
Lecture 29 Practice 10
Lecture 30 Practice 10 Answers
Lecture 31 Locus of a Half-line
Lecture 32 Practice 11
Lecture 33 Practice 11 Answers
Section 12: Inequalities in Complex Numbers (for IGCSE/College-Level)
Lecture 34 Inequalities in Complex Numbers
Lecture 35 Practice 12
Lecture 36 Practice 12 Answers
Section 13: De Moivre's Theorem (for IB HL/College-Level)
Lecture 37 De Moivre's Theorem
Lecture 38 Practice 13
Lecture 39 Practice 13 Answers
Section 14: Nth Roots of a Complex Number (for IB HL/College-Level)
Lecture 40 Nth Roots of a Complex Number
Lecture 41 Practice 14
Lecture 42 Practice 14 Answers
Section 15: Quiz 3
Section 16: Bonus! Problem-Solving Exercises, Solutions to Quizzes and an Extra Video!
Lecture 43 Complex Numbers Problem-Solving Exercises
Lecture 44 Answers to Problem-Solving Exercises
Lecture 45 Bonus! Correction of Argument to Principal Value
Lecture 46 Written Solutions to the Quizzes
Lecture 47 Further Problem-Solving Exercise 1
Lecture 48 Lecture 48: Further Problem-Solving Exercise 2
Section 17: Summary and Conclusions
Lecture 49 Summary and Conclusions
Students who are taking college-level mathematics,Students who are taking the IB HL Mathematics,Students who are taking the IGCSE/GCE 'A' level Mathematics,Students who need a good foundation in Complex Numbers for University-level modules