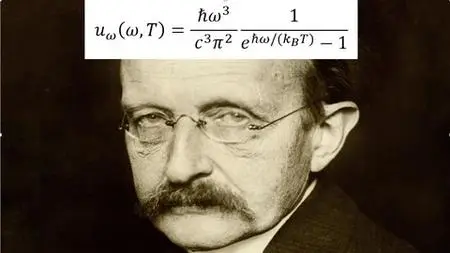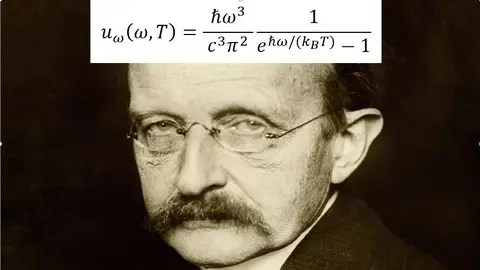Statistical Physics: Relation To Quanta And Thermodynamics

The mathematics used in the discovery of quantum physics, the foundations of thermodynamics, phase transitions.

What you'll learn

Planck's mathematical trick which led to the discovery of quantum physics

rigorous definition of entropy

history of the physics of the 1900's

Basics of Statistical Mechanics

Einstein's papers on thermodynamics

Brownian motion

Lioville theorem

Ideal gas law

photoelectric effect

canonical transformations

Hamilton equations

Black body problem

Phase transitions

Requirements

Calculus (especially derivatives, integrals, limits)

Multivariable Calculus

Basics of Fourier Analysis

For the second part of the course: Lagrange equations, phase space variables (position and momentum)

Description

First part of the course:The first part of the course showcases the beautiful mathematics that, in the late 19th century/ early 20th century, led to the discovery of a revolutionary branch in physics: Quantum Mechanics. Planck postulated that the energy of oscillators in a black body is quantized. This postulate was introduced by Max Planck in his derivation of his law of black body radiation in 1900. This assumption allowed Planck to derive a formula for the entire spectrum of the radiation emitted by a black body (we will also derive this spectrum in this course). Planck was unable to justify this assumption based on classical physics; he considered quantization as being purely a mathematical trick, rather than (as is now known) a fundamental change in the understanding of the world. In 1905, Albert Einstein adapted the Planck postulate to explain the photoelectric effect, but Einstein proposed that the energy of photons themselves was quantized (with photon energy given by the Planck–Einstein relation), and that quantization was not merely a "mathematical trick". Planck's postulate was further applied to understanding the Compton effect, and was applied by Niels Bohr to explain the emission spectrum of the hydrogen atom and derive the correct value of the Rydberg constant.In addition to the very useful mathematical tools that will be presented and discussed thoroughly, the students have the opportunity to learn about the historical aspects of how Planck tackled the blackbody problem.Calculus and multivariable Calculus are a prerequisite to the course; other important mathematical tools (such as: Fourier Series, Perseval's theorem, binomial coefficients, etc.) will be recalled, with emphasis being put on mathematical and physical insights rather than abstract rigor.Second part of the courseBy the end of June 1902, just after being accepted as Technical Assistant at the Federal Patent Office in Bern, Albert Einstein, 23, sent to the renowned journal Annalen der Physik a manuscript with the bold title “Kinetic Theory of Thermal Equilibrium and of the Second Law of Thermodynamics”. In the introduction, he explains that he wishes to fill a gap in the foundations of the general theory of heat, “for one has not yet succeeded in deriving the laws of thermal equilibrium and the second law of thermodynamics using only the equations of mechanics and the probability calculus”. He also announces “an extension of the second law that is of importance for the application of thermodynamics”. Finally, he will provide “the mathematical expression of the entropy from the standpoint of mechanics”. In particular, in the second part of the course we will see the mathematics Einstein used in his paper from 1902.Besides, other concepts from Classical mechanics are explained, such as Liouville's theorem (this theorem is used by Einstein in his article), as well as Hamilton equations and more.For the second part, the student should already be familiar with phase space and other concepts from classical physics (such as Lagrange equations).Third part of the courseIn the third part of the course some of the articles of Einstein's Annus Mirabilis are explained. In particular, the article on the photoelectric effect and that on the Brownian motion.Fourth part of the courseIn the last section of this course we focus on the derivation of phase transitons from the Ising model. All the previous sections will be useful in contextualizing this last part of the course.

Overview

Section 1: Introduction

Lecture 1 Introduction

Lecture 2 Introduction to the blackbody problem

Lecture 3 Definition of blackbody

Section 2: Analysis of blackbody cavities

Lecture 4 Irrelevance of Shape of the Cavity

Lecture 5 Wave equation for Electromagnetic Waves

Lecture 6 Solution to the Wave Equation

Lecture 7 Compliance with Boundary Conditions

Lecture 8 Number of Modes per Frequency

Lecture 9 Average Energy per Mode

Section 3: Quantization: Systems of Particles

Lecture 10 Distribution of the Average Energy, Planck's idea

Lecture 11 Systems of Particles, Binomial Coefficient

Lecture 12 Number of Arrangements of the Particles into the Energy Levels

Lecture 13 Sterling's Approximation

Lecture 14 Getting ready to maximize the Number of Arrangements

Section 4: Derivation of the Average Energy per Mode

Lecture 15 Maximizing the Number of Arrangements

Lecture 16 Expression for the Energy per Mode

Lecture 17 Planck's Mathematical Trick

Lecture 18 Calculation of the Average Energy per Mode part 1

Lecture 19 Calculation of the Average Energy per Mode part 2

Section 5: Derivation of the Stefan-Boltzman Law

Lecture 20 Classical vs Quantum

Lecture 21 Energy per Volume per Wavelength and Energy per Volume

Lecture 22 Planck's Integral

Lecture 23 Brief Summary of Fourier Analysis

Lecture 24 Parseval's Theorem

Lecture 25 Ultraviolet Catastrophe and Energy per Unit Surface

Lecture 26 Calculation of the Series 1/n^4

Lecture 27 Putting Results Together

Lecture 28 Deriving the Stefan-Boltzmann Law part1

Lecture 29 Deriving the Stefan-Boltzmann Law part2

Section 6: Useful appendix to the first part of the course

Lecture 30 Derivation of the Maxwell Boltzmann distribution

Lecture 31 Planck's idea for the mathematical solution to the black body problem

Lecture 32 How Planck derived the black-body radiation law the first time

Section 7: Einstein's article on thermodynamics from 1902

Lecture 33 The mathematics that Einstein used in one of his papers on thermodynamics part 1

Lecture 34 The mathematics that Einstein used in one of his papers on thermodynamics part 2

Lecture 35 The mathematics that Einstein used in one of his papers on thermodynamics part 3

Lecture 36 The mathematics that Einstein used in one of his papers on thermodynamics part 4

Lecture 37 The mathematics that Einstein used in one of his papers on thermodynamics part 5

Lecture 38 Mathematical proof of Liouville's theorem

Lecture 39 Canonical transformations and generating functions

Lecture 40 Hamilton equations derived from a variational principle

Lecture 41 Variation principle derived from Newton's second law

Lecture 42 Simple proof of Liouville's theorem

Lecture 43 Einstein's different approach for the derivation of the entropy

Lecture 44 Ideal gas law derived from Statistical Mechanics

Section 8: Einstein's article on the photoelectric effect, which ushered in Quantum Physics

Lecture 45 Part 1 of Einstein's article on the photoelectric effect

Lecture 46 Part 2 of Einstein's article on the photoelectric effect

Lecture 47 Part 3 of Einstein's article on the photoelectric effect

Lecture 48 Part 4 of Einstein's article on the photoelectric effect

Section 9: Einstein article on Brownian motion

Lecture 49 step-by-step explanation of Einstein's article on the Brownian motion

Section 10: Entropy derivation from Classical Mechanics

Lecture 50 part 1: Entropy as a Function of State and How to Derive it from Lagrange Eqs

Lecture 51 part 2: Entropy as a Function of State and How to Derive it from Lagrange Eqs

Lecture 52 part 3: Entropy as a Function of State and How to Derive it from Lagrange Eqs

Section 11: Phase transitions and the Ising model

Lecture 53 Ising model and effective free energy

Lecture 54 Mean field Theory in the Ising model

Lecture 55 Landau approach to phase transitions

Lecture 56 Discontinuity in the heat capacity

physics students,mathematics students,anyone interested in the historical fascinating origin of Quantum Physics,anyone interested in the mathematics used by Einstein in 1902 dealing with thermodynamics,anyone who seeks an in-depth understanding of entropy,Students who would like to improve their reasoning and insights in solving physical problems,anyone interested in explanations given through the lens of mathematics,engineering students