Mathematical Intuition Behind Differential Forms

Learn differential forms, wedge products, exterior derivatives, the Generalized Theorem of Calculus, Hodge dual, etc.

What you'll learn

Understanding the Fundamentals of Differential Forms

Exterior derivative

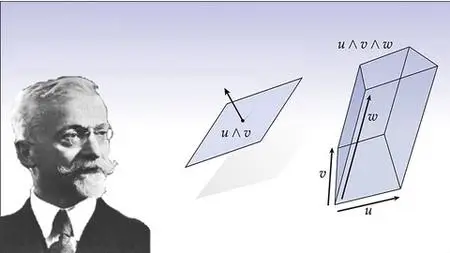
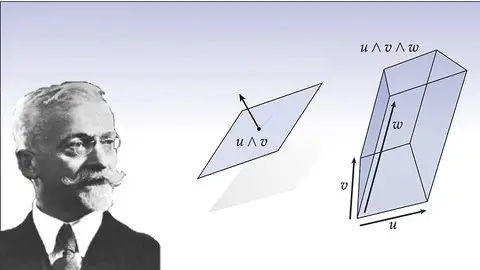
Wedge Product

Divergence theorem

Maxwell equations

Stokes' theorem

Hodge dual

Applying Differential Forms to Multivariable Calculus Problems

Applications to the electromagnetic field

Generalized Theorem of Calculus

Requirements

Basics of Calculus and Multivariable Calculus

Some knowledge of tensors (it would help understand differential forms more deeply)

Description

Get ready to understand the utility of differential forms in this course. Inspired by the work of Dubrovin, Fomenko, and Novikov, we'll explore the elegance of wedge products, differential forms, the generalized theorem of calculus, applications to electromagnetism, and more.No need to fear the math jargon – the aim of this course is to make it accessible and mathematically intuitive. Whether you're a math enthusiast or just curious, be part of this this journey to master the language of differential forms and its practical applications in both math and physics. Read the syllabus below.SyllabusModule 1: Introduction to Wedge Products1.1 Understanding BasicsIntroduction to formsNotation and terminologyMotivation for studying differential forms1.2 Wedge ProductsDefinition and propertiesIntuitive understandingApplications in geometryModule 2: Differential Forms and Fundamental Operations 2.1 Differential Forms and Exterior DerivativeDefinition and geometric interpretationProperties and examplesRelationship with differential forms2.2 Generalized Theorem of CalculusExtending calculus to differential formsModule 3: Examples with forms: Stoke's Theorem, Divergence Theorem, Theorem of Calculus3.1 Stoke's TheoremDerivation from differential formsPractical applications and examples3.2 Divergence TheoremConnection to differential formsVisualization and applicationsModule 4: Volume Elements, Second Exterior Derivative, Hodge dual4.1 Volume ElementsIntroduction and significanceCalculating volume elements in different coordinate systems4.2 Second Exterior derivativeProof that the iterated application of the exterior derivative leads to a zero result4.3 Hodge DualDefinition and propertiesHighlighting the invariant nature of the Hodge dualInspired by "Modern Geometry: Methods and Applications" by Dubrovin, Fomenko, NovikovModule 5: Applications in Physics5.1 Electromagnetic Field in Differential FormsFormulation of Maxwell's equations using differential formsDeriving the equations from first principlesPractical implications and insightsModule 6: ExercisesLearn how to apply the theory developed in the courseFurther reading:Suggested reading for deeper exploration: "Modern Geometry: Methods and Applications" by Dubrovin, Fomenko, Novikov.

Overview

Section 1: Introduction to differential forms

Lecture 1 Introductory video: overview of the course

Lecture 2 Generalization of the cross product and introduction to the wedge product

Lecture 3 Cross product in 2D derived from the wedge product

Lecture 4 Cross product in 3D derived from the wedge product

Lecture 5 Wedge product and degrees of forms

Lecture 6 Example: wedge product with 2-forms

Lecture 7 Relation between the wedge product and the triple product in 3D

Section 2: Differential Forms and Fundamental Operations

Lecture 8 Differential forms

Lecture 9 Exterior derivative

Lecture 10 Additional considerations on the exterior derivative in generic coordinates

Lecture 11 Examples of Exterior derivatives

Lecture 12 Overview of the Generalized Fundamental Theorem of Calculus

Lecture 13 Proof of the Generalized Fundamental Theorem of Calculus part 1

Lecture 14 Proof of the Generalized Fundamental Theorem of Calculus part 2

Section 3: Examples with forms: Stoke's Theorem, Divergence Theorem, Theorem of Calculus

Lecture 15 Example 1: application of the Generalized Theorem of Calculus

Lecture 16 Example 2: Stokes theorem in 2D derived from the Generalized Theorem of Calculus

Lecture 17 Example 3: Divergence Theorem derived from the Generalized Theorem of Calculus

Lecture 18 Example 4: Stokes Theorem derived from the Generalized Theorem of Calculus

Section 4: Volume Elements, Second Exterior Derivative, Hodge dual

Lecture 19 Transformation of volumes in the language of differential forms

Lecture 20 Invariant volume element in D dimensions

Lecture 21 Second exterior derivative of a form

Section 5: Applications to the Electromagnetic Field

Lecture 22 Application of differential forms to the electromagnetic field

Lecture 23 First Maxwell equation

Lecture 24 Second Maxwell equation

Lecture 25 Hodge dual, Levi Civita pseudo-tensor

Lecture 26 Exterior derivative of the Hodge dual of the electromagnetic form

Lecture 27 Derivation of the remaining Maxwell equations from differential forms

Section 6: Exercises with forms

Lecture 28 Exterior derivative of a wedge product of differential forms

Lecture 29 Exercise 1: calculation of the exterior derivative of a 2-form in 3D

Lecture 30 Exercise 2: calculation of the exterior derivative of a 1-form in 3D

Lecture 31 Exercise 3: calculation of the Hodge dual of a 1 form in 3D

Lecture 32 Observation on Hodge duals in 3D

Lecture 33 Calculation of a surface using differential forms

Lecture 34 Exercise with the Hodge dual in 2 dimensions

Mathematics Students,Physics Students,Engineering Students,Engineers: for example, those involved in fields such as aerospace, civil, or electrical engineering, seeking to enhance their mathematical toolkit for applications in modeling and problem-solving,Mathematicians,Physicists,Computer Science and Data Science Practitioners: Programmers, data scientists, or anyone working with algorithms and computational mathematics, looking to strengthen their understanding of mathematical structures that underpin advanced algorithms and data analysis techniques,Professionals in quantitative fields, such as finance or economics, who want to deepen their mathematical knowledge for career growth and improved problem-solving skills,Advanced High School Students: ambitious high school students with a strong foundation in calculus, eager to explore more sophisticated mathematical concepts that extend beyond the typical high school curriculum